
To avoid over-smoothing, we introduce a modified multiquadric approach that allows smooth, near-interpolation while maintaining the desirable shape-preserving properties of the data. This is usually noticeable at turning points and can occur when fitting the data using polynomials or cubic splines for example. When expanding data, for which the underlying smoothness properties are not known, there is often a danger of over-smoothing. We compare and contrast the effectiveness in reducing prediction error for three specific expansion models using radial basis function (RBF) kernels. This approach provides the learning algorithm with enough representative data to allow all of the parameters (premise and consequent) to be optimised. We propose a new approach, using robust data expansion methods to enhance the data carefully. In this paper, we address the problem of constructing accurate prediction models using ANFIS in circumstances where capturing large amounts of data is difficult. However, the scarcity of the data raises serious concerns when attempting to construct models of this type.
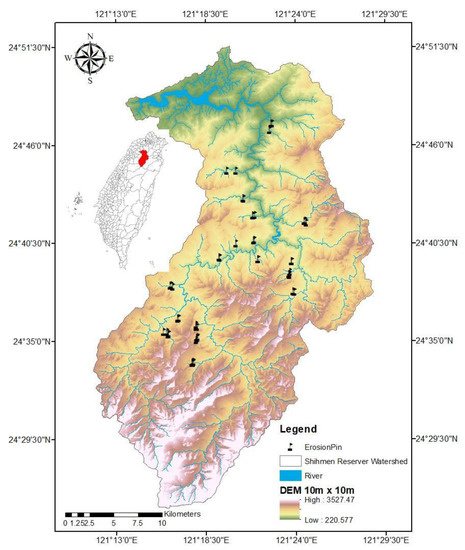
Due to the fuzzy nature of many data sets, it is appropriate to construct prediction models using fuzzy inference systems (FIS), rather than traditional artificial neural network (ANN) models.

Many real-world problems have limited data to work with and yet require models with high prediction accuracy. This work focuses on the problem of constructing accurate prediction models using an adaptive neuro-fuzzy inference system (ANFIS) from data that are scarce and poorly scaled.


 0 kommentar(er)
0 kommentar(er)
